Import Libraries

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import OPTICS
from sklearn import datasets
from kneed import KneeLocator
from matplotlib.patches import Polygon
import matplotlib.colors as mcolors
from scipy.spatial import ConvexHull

This block imports all necessary Python libraries. ‘numpy’ and ‘matplotlib’ are used for numerical operations and plotting(respectively). ‘sklearn’ provides the OPTICS clustering algorithm(for better or worse) and the blob generator. ‘kneed’ is used to identify the “knee”/“elbow” point of the data, but didn’t work in this case. We will explore alternatives below. ‘matplotlib.colors’ and ‘scipy.spatial’ help with the visualization and the convex hull calculations respectively.

Load and Visualize the Blob Data

# Load example data
n_samples = 1000
min_samples = 15
data, _ = datasets.make_blobs(n_samples=n_samples, centers=4, random_state=42, cluster_std=2.0)

# Plot the original data
plt.figure(figsize=(8, 6))
plt.scatter(data[:, 0], data[:, 1], alpha=0.6, edgecolors='w', s=30)
plt.title('Blob Data Distribution')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()

Synthetic blob data is generated using ‘make_blobs’ and we specify the number of points, centers(clusters) , random_state(for repeatability), and the cluster standard deviation(spread). The plot will help the user to get a feel for what the raw, unclustered data looks like. Keep in mind that we are using OPTICS to get to the “meat” of the cluster, there will be points identified as noise or otherwise of less significance than the core points.

Apply sklearn OPTICS Clustering

# Step 1: Apply OPTICS
optics_model = OPTICS(min_samples=min_samples)
optics_model.fit(data)

OPTICS(min_samples=15)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OPTICS(Ordering Points to Identify Clustering Structure) is an algorithm similar enough to DBSCAN, but handles varying densities better. This block will initialize the OPTICS model with a min sample count per cluster and fit it to the dataset. This will allow us to extract the reachability distances later on, which will quantify the density connectivity of the data points.

Get Reachability Distances & Handle Infinity Values

# Step 2: Plot the reachability diagram
space = np.arange(len(data))
reachability = optics_model.reachability_[optics_model.ordering_]

# Check for infinity values in reachability distances
if np.isinf(reachability).any():
    print("Infinity values found in reachability distances, handling...")
    # Identify finite indices where reachability values are not infinity
    finite_indices = np.isfinite(reachability)

    # Filter out infinite reachability values and their corresponding indices
    reachability = reachability[finite_indices]
    space = space[finite_indices]

plt.figure(figsize=(10, 5))
plt.bar(space, reachability, color='g')
plt.title('OPTICS Reachability Plot')
plt.xlabel('Data points')
plt.ylabel('Reachability Distance')
plt.show()

Infinity values found in reachability distances, handling...

This section will generate a plot of the unordered reachability distances and then further check that the reachability distances haven’t “exploded” to infinity. If they have they will be filtered out. the reachability plot is then plotted. Keep in mind that the reachability plot visualizes the distance at which each point becomes directly density-reachable from its predecessor in the ordered list. This will help you to understand the cluster structure and identify areas of high density(low reachability distance). You are looking for “waves” in which the reachability distance increases, drops off, and then begins to increase. Later on we will create an arbitrary cutoff for the reachability distance to identify each cluster.

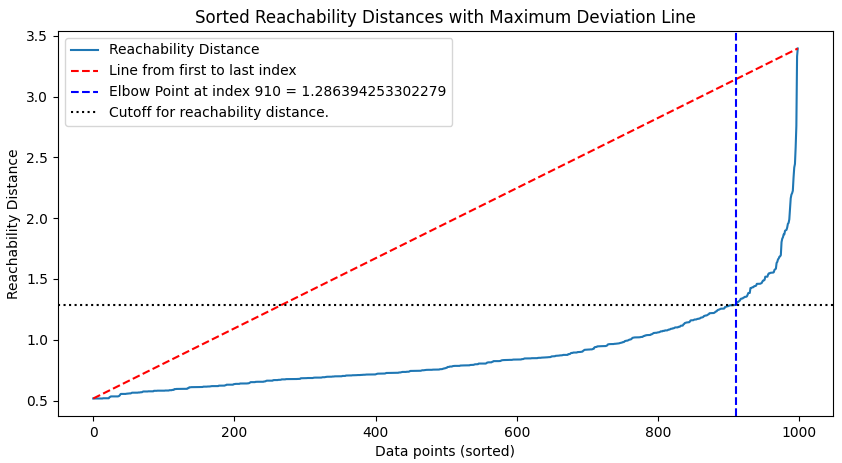
Identify the “Elbow” Point in the Sorted Reachability Plot

# Plot sorted reachability distances
sorted_reachability = np.sort(reachability)
indices = np.arange(len(sorted_reachability))
# plt.figure(figsize=(10, 5))
# plt.plot(indices, sorted_reachability, label='Reachability Distance')

# Compute the line endpoints based on the first and last reachability distance
line_start = np.array([0, sorted_reachability[0]])
line_end = np.array([len(sorted_reachability) - 1, sorted_reachability[-1]])

# Calculate the slope and intercept of the line (y = mx + b)
slope = (line_end[1] - line_start[1]) / (line_end[0] - line_start[0])
intercept = line_start[1] - (slope * line_start[0])

# Calculate the y-values of the line across all x-values
line_y = (slope * indices) + intercept

# Plot the line
# plt.plot(indices, line_y, 'r--', label='Line from first to last index')

# Find the elbow index (maximum deviation point)
deviations = np.abs(sorted_reachability - line_y)
elbow_index = np.argmax(deviations)

elbow_cutoff = sorted_reachability[elbow_index]


# Mark the elbow point
# plt.axvline(x=elbow_index, color='b', linestyle='--', label=f'Elbow Point at index {elbow_index} = {elbow_cutoff}')
# plt.axhline(y = elbow_cutoff, color = 'k', linestyle = ':', label = 'Cutoff for reachability distance.')
# plt.title('Sorted Reachability Distances with Maximum Deviation Line')
# plt.xlabel('Data points (sorted)')
# plt.ylabel('Reachability Distance')
# plt.legend()
# plt.show()

We plot the reachability distances sorted from least to greatest to get an idea of how the distribution looks. In this case we have a nice transition point where the distance explodes and that is roughly where we are aiming for our first “guess” of the reachability distance cutoff. We then implement a pretty basic algorithm wherein we find the maximum deviation point, that is the point farthest from the horizontal line drawn between the first and last reachability points. You will find a MATLAB based explaination here. Note that we do NOT use KneeLocator from the kneed library as it gives erroneous results in this case.

Trying the Maximum Deviation Line for Clustering

#  Create a list of colors to use for bars below the threshold, and black for above
# We'll generate a color map to cycle through a set of colors for segments below the threshold
below_threshold_colors = list(mcolors.TABLEAU_COLORS.values())  # Get a set of unique colors
color_index = 0
current_color = below_threshold_colors[color_index]
colors = []

# Track whether the previous bar was below the threshold
previous_bar_below = False

# Assign colors to bars based on their height relative to the threshold
for val in reachability:
    if val <= elbow_cutoff:
        # If we're transitioning from above to below the threshold, change the color
        if not previous_bar_below:
            color_index = (color_index + 1) % len(below_threshold_colors)
            current_color = below_threshold_colors[color_index]
        colors.append(current_color)
        previous_bar_below = True
    else:
        colors.append('k')  # Black for bars above the threshold
        previous_bar_below = False

# Now, let's create the reachability plot with custom bar colors
# plt.figure(figsize=(10, 5))
# plt.axhline(y=elbow_cutoff, color='k', linestyle=':', label='Cutoff for reachability distance.')
# plt.bar(space, reachability, color=colors)
# plt.title('OPTICS Reachability Plot')
# plt.xlabel('Data points')
# plt.ylabel('Reachability Distance')
# plt.legend()
# plt.show()

# Step 3: Extract clusters using the reachability distance at the elbow point as a cutoff
# The reachability distance at the elbow is used as a threshold for cluster extraction
reachability_distance_at_elbow = elbow_cutoff

# Retrieve the ordered reachability distances from the OPTICS model
ordered_reachability = optics_model.reachability_[optics_model.ordering_]
ordered_indices = optics_model.ordering_

# Initialize all points as noise (-1)
labels = np.full(ordered_reachability.shape, -1)  

# Manually assign clusters based on the new threshold, apparently OPTICS.expand_clusters or similar doesn't work anymore so here we are...
cluster_id = 0
for i in range(len(ordered_reachability)):
    if ordered_reachability[i] <= reachability_distance_at_elbow:
        if labels[ordered_indices[i]] == -1:  # If this point has not been assigned a cluster
            # Start a new cluster from this point
            labels[ordered_indices[i]] = cluster_id
            # Add all directly reachable points to the same cluster
            for j in range(i + 1, len(ordered_reachability)):
                if ordered_reachability[j] <= reachability_distance_at_elbow:
                    labels[ordered_indices[j]] = cluster_id
                else:
                    break
            cluster_id += 1

# Step 4: Plot the clusters based on the new manually set labels
# plt.figure(figsize=(10, 7))
unique_labels = set(labels)

# Generate colors for each cluster label
colors = plt.cm.rainbow(np.linspace(0, 1, len(unique_labels)))

# for klass, color in zip(unique_labels, colors):
#     class_member_mask = (labels == klass)
#     xy = data[class_member_mask]
#     if klass != -1:
#         # Draw the convex hull and fill it with a light shade of the cluster color
#         if xy.shape[0] > 2:  # ConvexHull needs at least 3 points to compute the hull
#             hull = ConvexHull(xy)
#             plt.fill(xy[hull.vertices, 0], xy[hull.vertices, 1], color=color, alpha=0.2, edgecolor='k')
#         plt.scatter(xy[:, 0], xy[:, 1], color=color, edgecolor='k', label=f'Cluster {klass}')
#     else:
#         plt.scatter(xy[:, 0], xy[:, 1], c='k', marker='x', label='Noise')

# plt.title('Clusters by OPTICS with Manual Threshold and Hulls')
# plt.xlabel('Feature 1')
# plt.ylabel('Feature 2')
# plt.legend()
# plt.show()

As you can see above we get three clusters based on one of the clusters encountering significant overlap. We can stop here and examine why this may be when we don’t have synthetic data, but at least for the purposes of this demonstration I will find the point at which I need to set the reachability distance to distinguish that first cluster by hovering over that point in Python’s matplotlib plot. As you can see below that value is roughly 0.88 . See that all we have to do is change one line and we can rerun the reachability distance.

elbow_cutoff =0.866 ##THIS IS A GREAT EXAMPLE OF WHEN YOUR ELBOW FAILS YOU AND YOU NEED TO PLAY AROUND WITH VALUES!!!!

#  Create a list of colors to use for bars below the threshold, and black for above
# We'll generate a color map to cycle through a set of colors for segments below the threshold
below_threshold_colors = list(mcolors.TABLEAU_COLORS.values())  # Get a set of unique colors
color_index = 0
current_color = below_threshold_colors[color_index]
colors = []

# Track whether the previous bar was below the threshold
previous_bar_below = False

# Assign colors to bars based on their height relative to the threshold
for val in reachability:
    if val <= elbow_cutoff:
        # If we're transitioning from above to below the threshold, change the color
        if not previous_bar_below:
            color_index = (color_index + 1) % len(below_threshold_colors)
            current_color = below_threshold_colors[color_index]
        colors.append(current_color)
        previous_bar_below = True
    else:
        colors.append('k')  # Black for bars above the threshold
        previous_bar_below = False

# Now, let's create the reachability plot with custom bar colors
plt.figure(figsize=(10, 5))
plt.axhline(y=elbow_cutoff, color='k', linestyle=':', label='Cutoff for reachability distance.')
plt.bar(space, reachability, color=colors)
plt.title('OPTICS Reachability Plot')
plt.xlabel('Data points')
plt.ylabel('Reachability Distance')
plt.legend()
plt.show()

Now that we have broken out the clusters we can now reassign clusters based on the new threshold.

# Step 3: Extract clusters using the reachability distance at the elbow point as a cutoff
# The reachability distance at the elbow is used as a threshold for cluster extraction
reachability_distance_at_elbow = elbow_cutoff

# Retrieve the ordered reachability distances from the OPTICS model
ordered_reachability = optics_model.reachability_[optics_model.ordering_]
ordered_indices = optics_model.ordering_

# Initialize all points as noise (-1)
labels = np.full(ordered_reachability.shape, -1)  

# Manually assign clusters based on the new threshold, apparently OPTICS.expand_clusters or similar doesn't work anymore so here we are...
cluster_id = 0
for i in range(len(ordered_reachability)):
    if ordered_reachability[i] <= reachability_distance_at_elbow:
        if labels[ordered_indices[i]] == -1:  # If this point has not been assigned a cluster
            # Start a new cluster from this point
            labels[ordered_indices[i]] = cluster_id
            # Add all directly reachable points to the same cluster
            for j in range(i + 1, len(ordered_reachability)):
                if ordered_reachability[j] <= reachability_distance_at_elbow:
                    labels[ordered_indices[j]] = cluster_id
                else:
                    break
            cluster_id += 1

# Step 4: Plot the clusters based on the new manually set labels
# plt.figure(figsize=(10, 7))
unique_labels = set(labels)

# Generate colors for each cluster label
colors = plt.cm.rainbow(np.linspace(0, 1, len(unique_labels)))

# for klass, color in zip(unique_labels, colors):
#     class_member_mask = (labels == klass)
#     xy = data[class_member_mask]
#     if klass != -1:
#         # Draw the convex hull and fill it with a light shade of the cluster color
#         if xy.shape[0] > 2:  # ConvexHull needs at least 3 points to compute the hull
#             hull = ConvexHull(xy)
#             plt.fill(xy[hull.vertices, 0], xy[hull.vertices, 1], color=color, alpha=0.2, edgecolor='k')
#         plt.scatter(xy[:, 0], xy[:, 1], color=color, edgecolor='k', label=f'Cluster {klass}')
#     else:
#         plt.scatter(xy[:, 0], xy[:, 1], c='k', marker='x', label='Noise')

# plt.title('Clusters by OPTICS with Manual Threshold and Hulls')
# plt.xlabel('Feature 1')
# plt.ylabel('Feature 2')
# plt.legend()
# plt.show()

And that’s it. Given this data and the significant overlap between cluster’s 0 and 1 I would definitely just go with the original reachability distance found by the elbow, but given that we have ZERO underlying knowledge besides here’s 4 clusters here we are. Note that the ratio of noise:data changed and more points are discarded. Evaluate whether or not those points are important and if so consider other clustering algorithms(I’m looking at you Esimation Maximization). For an example with differing STD see here.

If we want to use the Xi clustering method on this data by evaluating the relative slopes of the reachability plot or by evaluating the silhouette score of a variety of Xi values we can proceed with the below. Please note that we use the same data as before.

#Now instead of using the reachability metric we use the Xi clustering method to apply OPTICS
#Please note I tried relative differences in reachability distances by calculating their relative slopes and another method using significant slopes
# using a percentile approach and they both performed poor.
from sklearn.metrics import silhouette_score
from joblib import Parallel, delayed #I have 16 cores and I will use 16 cores....
# Initial OPTICS model to get reachability distances
optics_model_initial = OPTICS(min_samples=min_samples)
optics_model_initial.fit(data)
reachabilities_initial = optics_model_initial.reachability_[optics_model_initial.ordering_]

# Calculate differences in reachability distances
reachability_diffs = np.diff(reachabilities_initial)
reachability_diffs = reachability_diffs[np.isfinite(reachability_diffs)]  # Remove any infinite or NaN values

# Validate differences before calculating statistics
if len(reachability_diffs) > 0:
    mean_diff = np.mean(reachability_diffs)
    std_diff = np.std(reachability_diffs)
    xi_value = max(0.0, min(mean_diff + std_diff, 1.0))  # Ensure Xi is within [0.0, 1.0] and not NaN
else:
    xi_value = 0.05  # Fallback value if differences calculation fails
print("Xi Value[Differences]:", xi_value)

# Calculate relative slopes (normalized by preceding reachability value)
slopes = np.diff(reachabilities_initial) / reachabilities_initial[:-1]
# print(slopes)
# Handle any NaN or infinity from division by very small numbers
slopes = np.nan_to_num(slopes)

# Determine significant slopes using a percentile approach
significant_slope_threshold = np.percentile(np.abs(slopes), 96)
print(significant_slope_threshold)
# Use this threshold to set Xi
xi_value = significant_slope_threshold
print("Xi_value[Significanty Slopes]: ", xi_value)



#Rewrite Me

# Define a function that computes the silhouette score for a given Xi
def compute_silhouette(xi, data, min_samples):
    model = OPTICS(min_samples=min_samples, xi=xi, cluster_method='xi')
    model.fit(data)
    labels = model.labels_
    if len(set(labels)) > 1 and np.any(labels != -1):
        return silhouette_score(data, labels)
    else:
        return -1  # Return a penalty for bad clustering
    
# Trying a range of potential Xi values to find the best based on silhouette score
xi_values = np.linspace(0.01, 1, 1000)  # Testing Xi values from 0.01 to 0.1

#Note this can take some time to calculate...
silhouette_scores = []
#Silhouette score is a metric used to evaluate the quality of clustering.Aim for highest silhouette score.

# Use joblib to parallelize the computation of silhouette scores. Update article.
silhouette_scores = Parallel(n_jobs=-1)(delayed(compute_silhouette)(xi, data, min_samples) for xi in xi_values)

# Plot the silhouette scores for different Xi values
# plt.figure(figsize=(10, 5))
# plt.plot(xi_values, silhouette_scores, marker='o')
# plt.title('Silhouette Scores for Different Xi Values')
# plt.xlabel('Xi Value')
# plt.ylabel('Silhouette Score')
# plt.grid(True)
# plt.show()

Xi Value[Differences]: 0.06738467759335512
0.06486873356523164
Xi_value[Significanty Slopes]:  0.06486873356523164

C:\Users\Jesse\AppData\Local\Temp\ipykernel_282880\2141299887.py:25: RuntimeWarning: invalid value encountered in divide
  slopes = np.diff(reachabilities_initial) / reachabilities_initial[:-1]

As one can see in the image above, the silhouette score is maximized at a value of: 0.1725225…. and thus that is what we will use. The silhouette score is a measure of how similar an object is to its own cluster compared to other clusters. This metric ranges from -1 to +1, where a high value indicates that the object is well matched to its own cluster and poorly matched to neighboring clusters. A score close to 1 signifies that the object is far away from its neighboring clusters, a score of 0 indicates that the object is on or very close to the decision boundary between two neighboring clusters, and a negative score indicates that the object might have been assigned to the wrong cluster. From here we will select the best Xi to use based on the maximum silhouette score.

# Select the best Xi based on maximum silhouette score
best_xi_index = np.argmax(silhouette_scores)
best_xi = xi_values[best_xi_index]
xi_value = best_xi
print("Xi Value[Silhouette Score Iterative]", xi_value)
# Apply OPTICS using dynamically determined xi clustering method
optics_model = OPTICS(min_samples=min_samples, xi=xi_value, cluster_method='xi')
optics_model.fit(data)

# Extract the clusters using the xi method
labels = optics_model.labels_

# Reachability plot
reachabilities = optics_model.reachability_[optics_model.ordering_]
space = np.arange(len(data))

# plt.figure(figsize=(12, 6))
# plt.bar(space, reachabilities, color='g')
# plt.title('OPTICS Reachability Plot with Dynamic Xi Clustering')
# plt.xlabel('Ordered Data Points')
# plt.ylabel('Reachability Distance')
# plt.show()

# Plot the clusters
unique_labels = set(labels)

# Generate colors for each cluster label
colors = plt.cm.rainbow(np.linspace(0, 1, len(unique_labels)))
cluster_colors = [colors[list(unique_labels).index(label)] if label != -1 else 'k' for label in labels[optics_model.ordering_]]

# plt.figure(figsize=(12, 6))
# plt.bar(space, reachabilities, color=cluster_colors)
# plt.title('OPTICS Reachability Plot with Cluster Coloring and Dynamic Xi')
# plt.xlabel('Ordered Data Points')
# plt.ylabel('Reachability Distance')
# plt.show()

Xi Value[Silhouette Score Iterative] 0.17252252252252254

As one can see the number of clusters is different here and more likely than not indicative of my ability/willingness to play with Xi values than the inherent performance of OPTICS. Regardless, it was much faster to simply establish a cutoff with the first method described than it was to iterate over Xi for this particular dataset. There may be cases where Xi is better equipped to cluster the dataset and as a result I kept it here for my own reference sometime in the future.

The resultant clustering is performed below:

# Scatter plot of clusters
# plt.figure(figsize=(10, 7))

# for klass, color in zip(unique_labels, colors):
#     class_member_mask = (labels == klass)
#     xy = data[class_member_mask]
#     if klass != -1:
#         # Draw the convex hull and fill it with a light shade of the cluster color
#         if xy.shape[0] > 2:  # ConvexHull needs at least 3 points to compute the hull
#             hull = ConvexHull(xy)
#             plt.fill(xy[hull.vertices, 0], xy[hull.vertices, 1], color=color, alpha=0.2, edgecolor='k')
#         plt.scatter(xy[:, 0], xy[:, 1], color=color, edgecolor='k', label=f'Cluster {klass}')
#     else:
#         plt.scatter(xy[:, 0], xy[:, 1], c='k', marker='x', label='Noise')

# plt.title('Clusters by OPTICS with Dynamically Determined Xi and Hulls')
# plt.xlabel('Feature 1')
# plt.ylabel('Feature 2')
# plt.legend()
# plt.show()

Finally, I got a little bit more neurotic and decided to iteratively vary Xi and analyze a number of metrics including the Silhouette Score, Davies-Bouldin Index, Calinski-Harabasz Index(Variance Ratio Criterion), the Adjusted Rand Index, and Mutual Information. A short description of each is below:

Silhouette Score: This metric evaluates how well each data point fits within its assigned cluster compared to other clusters. A high silhouette value indicates that the point is well matched to its own cluster and poorly matched to neighboring clusters, with values ranging from -1 (poor clustering) to +1 (excellent clustering).
Davies-Bouldin Index: An internal evaluation scheme where lower values indicate better clustering. It measures the average ‘similarity’ between each cluster and the cluster most similar to it, where similarity is a ratio of within-cluster distances to between-cluster distances.
Calinski-Harabasz Index (Variance Ratio Criterion): This index is a ratio of the sum of between-clusters dispersion and within-cluster dispersion for all clusters. Essentially, it evaluates clusters by how well-separated they are and how compact they are, with higher values generally indicating better-defined clusters.
Adjusted Rand Index: This is a measure of the similarity between two data clusterings. It is adjusted for chance, providing a value that denotes random labeling independently of the number of clusters and samples. It ranges from -1 to +1, where higher values indicate better agreement between clustering assignments.
Mutual Information: This measures the amount of information one can obtain about one random variable by observing another random variable. The Adjusted Mutual Information (AMI) score is an adjustment of the Mutual Information Score that accounts for chance, making it a more reliable metric in assessing the agreement of the clustering result with the ground truth, if available. This one is really just thrown because why not?

The code is below and I parallelized the calculations as it would have taken quite some time otherwise.

# Neuroticism:

from sklearn.metrics import davies_bouldin_score, calinski_harabasz_score, adjusted_rand_score, adjusted_mutual_info_score
from joblib import Parallel, delayed #I have 16 cores and I will use 16 cores....

# Define the function to compute all metrics
def compute_metrics(xi, data, labels_true):
    model = OPTICS(min_samples=min_samples, xi=xi, cluster_method='xi')
    model.fit(data)
    labels = model.labels_
    
    # Calculate metrics only if valid clustering is formed
    if len(set(labels)) > 1 and np.any(labels != -1):
        sil_score = silhouette_score(data, labels)
        db_score = davies_bouldin_score(data, labels)
        ch_score = calinski_harabasz_score(data, labels)
        ar_score = adjusted_rand_score(labels_true, labels)
        mi_score = adjusted_mutual_info_score(labels_true, labels)
    else:
        sil_score = db_score = ch_score = ar_score = mi_score = -1  # Penalty for bad or invalid clustering
    
    return (sil_score, db_score, ch_score, ar_score, mi_score)

# Range of Xi values
xi_values = np.linspace(0.01, 1, 1000)  # Using 20 Xi values for demonstration

# Parallel computation of metrics
results = Parallel(n_jobs=-1)(delayed(compute_metrics)(xi, data, labels) for xi in xi_values)

# Extract the results
silhouette_scores, db_scores, ch_scores, ar_scores, mi_scores = zip(*results)

# # Plotting all the metrics
# fig, axs = plt.subplots(5, 1, figsize=(10, 25))

# # Silhouette Score
# axs[0].plot(xi_values, silhouette_scores, marker='o')
# axs[0].set_title('Silhouette Score vs Xi')
# axs[0].set_xlabel('Xi')
# axs[0].set_ylabel('Silhouette Score')

# # Davies-Bouldin Score
# axs[1].plot(xi_values, db_scores, marker='o')
# axs[1].set_title('Davies-Bouldin Score vs Xi')
# axs[1].set_xlabel('Xi')
# axs[1].set_ylabel('Davies-Bouldin Score')

# # Calinski-Harabasz Index
# axs[2].plot(xi_values, ch_scores, marker='o')
# axs[2].set_title('Calinski-Harabasz Index vs Xi')
# axs[2].set_xlabel('Xi')
# axs[2].set_ylabel('Calinski-Harabasz Index')

# # Adjusted Rand Index
# axs[3].plot(xi_values, ar_scores, marker='o')
# axs[3].set_title('Adjusted Rand Index vs Xi')
# axs[3].set_xlabel('Xi')
# axs[3].set_ylabel('Adjusted Rand Score')

# # Mutual Information
# axs[4].plot(xi_values, mi_scores, marker='o')
# axs[4].set_title('Mutual Information vs Xi')
# axs[4].set_xlabel('Xi')
# axs[4].set_ylabel('Mutual Information Score')

# plt.tight_layout()
# plt.show()

# Normalize scores
# Invert Davies-Bouldin scores since lower is better
db_scores = 1 / np.array(db_scores)

# Normalize all scores to be between 0 and 1
silhouette_norm = (silhouette_scores - np.min(silhouette_scores)) / (np.max(silhouette_scores) - np.min(silhouette_scores))
db_norm = (db_scores - np.min(db_scores)) / (np.max(db_scores) - np.min(db_scores))
ch_norm = (ch_scores - np.min(ch_scores)) / (np.max(ch_scores) - np.min(ch_scores))
ar_norm = (ar_scores - np.min(ar_scores)) / (np.max(ar_scores) - np.min(ar_scores))
mi_norm = (mi_scores - np.min(mi_scores)) / (np.max(mi_scores) - np.min(mi_scores))

# Assume equal weighting for simplicity, sum normalized scores
weighted_scores = silhouette_norm + db_norm + ch_norm + ar_norm + mi_norm

# Find the Xi with the highest weighted score
optimal_xi_index = np.argmax(weighted_scores)
optimal_xi = xi_values[optimal_xi_index]

# # Plot each metric
# fig, ax = plt.subplots(5, 1, figsize=(10, 20))
# ax[0].plot(xi_values, silhouette_norm, label='Silhouette Score')
# ax[1].plot(xi_values, db_norm, label='Davies-Bouldin Index')
# ax[2].plot(xi_values, ch_norm, label='Calinski-Harabasz Score')
# ax[3].plot(xi_values, ar_norm, label='Adjusted Rand Index')
# ax[4].plot(xi_values, mi_norm, label='Adjusted Mutual Information')

# for a in ax:
#     a.set_xlabel('Xi Value')
#     a.set_ylabel('Normalized Score')
#     a.legend()
#     a.grid(True)

# plt.tight_layout()
# plt.show()

# Normalize and invert scores where necessary
silhouette_norm = (silhouette_scores - np.min(silhouette_scores)) / (np.max(silhouette_scores) - np.min(silhouette_scores))
db_norm = 1 - ((db_scores - np.min(db_scores)) / (np.max(db_scores) - np.min(db_scores)))
ch_norm = (ch_scores - np.min(ch_scores)) / (np.max(ch_scores) - np.min(ch_scores))
ar_norm = (ar_scores - np.min(ar_scores)) / (np.max(ar_scores) - np.min(ar_scores))
mi_norm = (mi_scores - np.min(mi_scores)) / (np.max(mi_scores) - np.min(mi_scores))

# Calculate the average Xi from the max indices
optimal_indices = [np.argmax(silhouette_norm), np.argmax(db_norm), np.argmax(ch_norm), np.argmax(ar_norm), np.argmax(mi_norm)]
optimal_xis = xi_values[optimal_indices]
average_xi = np.mean(optimal_xis)

print("Optimal Xi values from each metric:", optimal_xis)
print("Average Optimal Xi:", average_xi)

Optimal Xi values from each metric: [0.17252252 0.26666667 0.04963964 0.17252252 0.17252252]
Average Optimal Xi: 0.1667747747747748

Here are the scores:

And the resultant clustering:

As you can see the data gets segmented into 2 distinct clusters. Interestingly enough the values obtained for the metrics are below:

Metrics, Score Normalized, Xi Value
Metric	Xi
Silhouette Score	0.17252252
Davies-Bouldin Index	0.26666667
Calinski-Harabasz Index (Variance Ratio Criterion)	0.04963964
Adjusted Rand Index	0.05459459
Mutual Information	0.05459459

If we omit the Silhouette Score and Davies-Bouldin Index we get the resulting clustering:

This can be viewed as an improvement if the upper left cluster could be considered sparse enough to be considered noise/irrelevant.

Overall, I could see how Xi could be useful in clustering datasets, but I definitely prefer to extract a DBSCAN-like clustering from an OPTICS model and work with that as its pretty fast. Iteratively using Xi has been outlined here and if I ever come across a use case this will be a pretty good reference.

And there you have it. Original code here.

OPTICS in Python